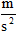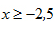| Opgave 1 |
|||||||||||||||||||||||||||||||||||||
| Hallen, som ses på billedet nedenfor, består af et par lodrette vægge og gavle og et tag, som består af to plane flader. |
|||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||
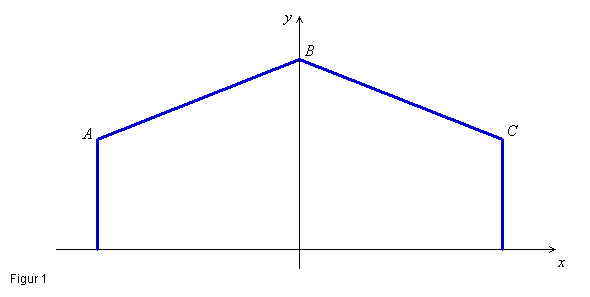
På nedenstående link kan du se hele hallen i panorering. Panorering På figur 1 ses et snit gennem hallen lagt ind i et koordinatsystem. Koordinaterne til punkterne A, B og C angives i meter og er indvendige mål i hallen. |
|||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||
x og y bestemmes på baggrund af dette program, hvor du skal indtaste din fødselsdato (dag, måned). A(-x;5,50) B(0;y) C(x;5,50) a) Bestem tagets vinkel med vandret. |
|||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||
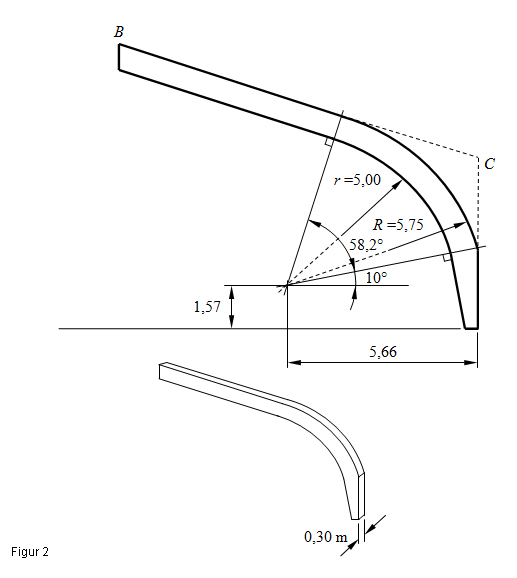
Som det fremgår af billedet ovenfor, bæres hallens tag af buer. Buerne er fremstillet af limtræ. En simplificeret model af en limtræsbue kan ses på figur 2, hvor alle mål er i meter. Limtræsbuernes tykkelse er 0,30 meter. |
|||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||
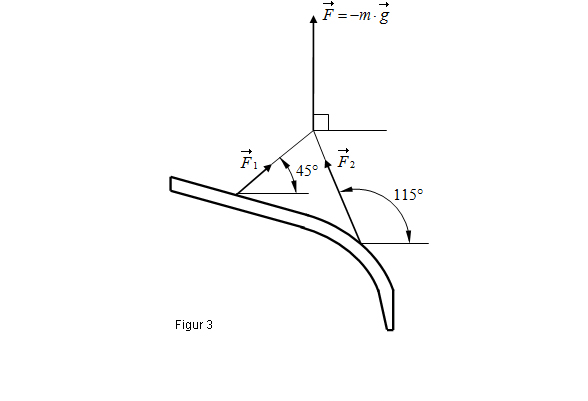
b) Bestem massen af den viste limtræsbue, når det oplyses, at densiteten for limtræ kan sættes til 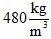 En limtræsbue magen til den, du lige har beregnet massen af, skal indgå i en ny hal, som er ved at blive bygget. Limtræsbuen løftes på plads med kran i et par wirer, som er sat fast på limtræsbuen. Placering af wirerne kan ses på figur 3. Tyngdekraften på limtræsbuen beregnes på følgende måde: 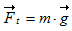
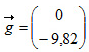 For at løfte limtræsbjælken skal kranen løfte med en kraft, kaldet 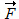 , som er lige så stor men , som er lige så stor menmodsat rettet tyngdekraften. Når bjælken hænger stille er kræfterne i balance. Kræfterne, og vinklerne de danner med vandret, kan ses på figur 3. |
|||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||
c) Bestem størrelsen og koordinaterne til kræfterne 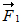 og og 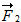 vist på figur 3. vist på figur 3. |
|||||||||||||||||||||||||||||||||||||
Hallen bruges meget ofte til badminton, så derfor ønskes nogle forskellige forhold analyseret og beregnet. Hvis du klikker på nedenstående link, kan du se, hvorledes en badmintonbold bevæger sig ved en lang serv. Lang serv Hvis der lægges et koordinatsystem ind i et snit langs badmintonbanen, således at badmintonbanens midte befinder sig i (0;0) kan man tilnærmelsesvis beskrive boldens bane ved følgende funktion, hvor y-koordinaten angiver boldens højde over gulvet målt i meter. |
|||||||||||||||||||||||||||||||||||||
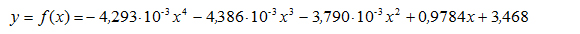 |
|||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||
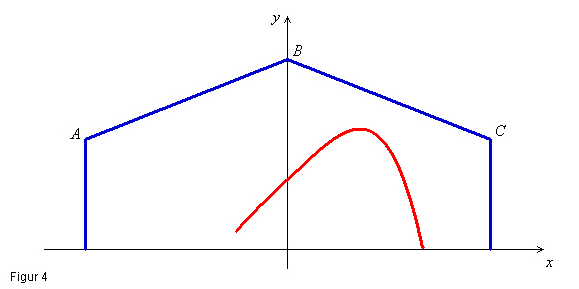
I det indlagte koordinatsystem, som ses i figur 4, rammer den servende badmintonspiller bolden hvor x = –2,5. d) I hvilken højde rammer badmintonspilleren badmintonbolden? e) Bestem x-koordinaten til stedet hvor badmintonbolden lander efter serven. f) Bestem den maksimale højde som badmintonbolden opnår ved den lange serv. Badmintonbolden må naturligvis ikke ramme loftet under serven og skal helst heller ikke komme for tæt på loftet, svarende til linjestykket BC på figur 4. g) Bestem badmintonboldens mindste afstand til loftet. I de foregående opgaver arbejdede du med den lange badmintonserv. Denne type serv benyttes ofte når man spiller single. I doublespillet benyttes oftere den korte serv. Hvis du klikker på nedenstående link, kan du se, hvorledes en badmintonbold bevæger sig ved en kort serv. Kort serv Der lægges et koordinatsystem ind i et snit langs badmintonbanen, hvor y-koordinaten angiver boldens højde over gulvet. En analyse af en kort serv, svarende til den på videoklippet, giver de data, som er vist i tabel 1. |
|||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
|
h) Ved hjælp af data fra tabellen skal du bestemme en tilnærmet værdi for den længde, badmintonbolden i) Bestem en tilnærmet værdi for den vinkel bolden vil ramme gulvet med. |
|||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||
|
Idrætsforeningen ønsker også at indrette hallen til basketball. Derfor skal der tegnes endnu en baneopmærkning på gulvet. |
|||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||
|
Målene på en basketballbane kan ses på figur 5, hvor alle mål er i meter. |
|||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||
|
j) Læg basketballbanen ind i et koordinatsystem og beskriv analytisk alle linjestykker, cirkler og cirkelbuer, |